Heron of Alexandria (c. 10–85 AD); an experimental scientist and inventor of steam turbines, wind powered machines & automatic vending machines

This post is a short tribute to Heron of Alexandria, one of the pioneers of Technology in Hellenistic times.

Abstract Heron of Alexandria was a mathematician, physicist and engineer who lived around 10–85 AD. He taught at Alexandria’s Musaeum and wrote many books on Mathematics, Geometry and Engineering, which were in use till the medieval times. His most important invention was the Aeolipile, the first steam turbine. Other inventions include automated machines for temples and theaters, surveying instruments, and military machines and weapons.

The ancient Greek technology developed mostly in the period 300 BC to 150 AD and was in use for more than one thousand years. It had a profound impact both on Western and Muslim civilization. Notable inventions include cranes, screws, gears, organs, odometer, dial and pointer devices, wheelbarrows, diving bells, parchment, crossbows, torsion catapults, rutways, showers, roof tiles, breakwaters, and many more. Greek engineers were pioneers in three of the first four means of non-human propulsion known prior to the Industrial Age: watermills, windmills, and steam engines, although only water power was used extensively, (Lahanas, Web). Among the Ancient Greek Engineers, the most prominent include Archimedes, Ktesibios, Heron, and Pappos.

Heron (or Hero) lived in the Hellenistic times in Alexandria, Egypt, at that time part of the Roman empire. He was made famous for documenting the first steam turbine, the aelolipile. He also invented many mechanisms for temples and theaters while he advanced or improved inventions by others, for example the hydraulis, originally invented by Ktesibius. Heron was also called Michanikos, the Greek word for Engineer.

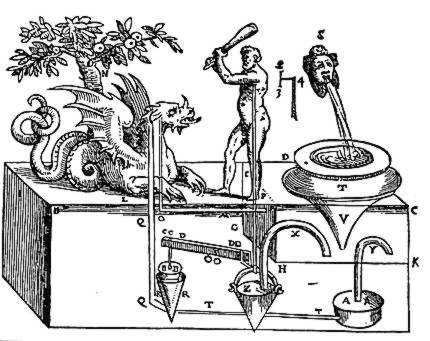
It is important to stress that in the Ancient World, technology was not considered as very important for the growth of philosophy and science. The dominant motive in philosophy was understanding or wisdom, while the connection between science and technology was not as extensive as it is today. In this context, Heron, as well as the other engineers, were on the exception side (Lloyd, 1991).

According to Drachmann (1963), Heron was a man who knew his business thoroughly, who was a skillful mathematician, astronomer, engineer and inventor of his time. Based on the content of the book Pneumatica, a number of researchers expressed doubts about his capabilities. However, this book appears to be an unfinished collection of notes and may have been altered through the years.

An important characteristic of Heron’s work was clarity in expressing his ideas, something not common in ancient writings. As Drachmann (1963) states, “a man who is always able to present his subject in such a way that is readily understood, is a man who understands it himself, and he is certainly not a fool or a bungler.”

In many of his works, Heron would start by reviewing past works. However, he would not always give credit to previous inventors and would tend to dismiss easily the work of others, before presenting his own solutions.

Heron recognized the value of experimental work. The example passage, taken from Lloyd (1973), attacks first those (like Aristotle) who denied absolutely that a void can exist, accusing them of following their faith as opposed to evidence:

Those then who assert generally that there is no vacuum are satisfied with inventing many arguments for this and perhaps seeming plausible with their theory in the absence of sensible proof. If, however, by referring to the appearances and to what is accessible to sensation, it is shown that there is a continuous vacuum, but only one produced contrary to nature; that there is a natural vacuum, but one scattered in tiny quantities; and that bodies fill up these scattered vacua by compression; then those who put forward plausible arguments on these matters will no longer have any loop-hole.

Unlike other ancient works in Greek, the language in Heron’s book is quite easy to be read by non-scholars, even today. Except the Definitiones, these books mostly consist of methods for obtaining the areas and volumes, of plane or solid figures. In these, Heron gave methods for computing very close approximations to the square roots of numbers, which are not complete squares and even cubic roots of numbers, which are not complete cubes. Heron also provided expressions for computing the areas of regular polygons of five to twelve sides in terms of the squares of the sides that lead to important trigonometrical ratio approximations.

(Source: “Heron of Alexandria (c. 10–85 AD)”, by Evangelos Papadopoulos)

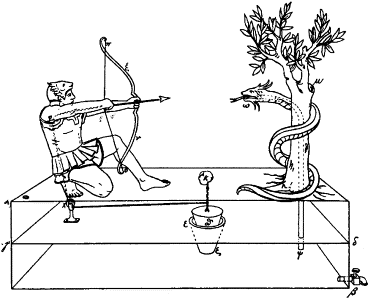
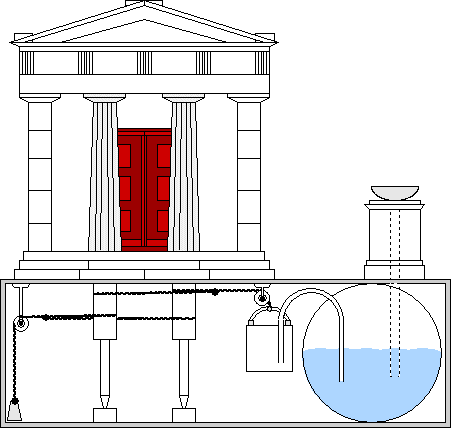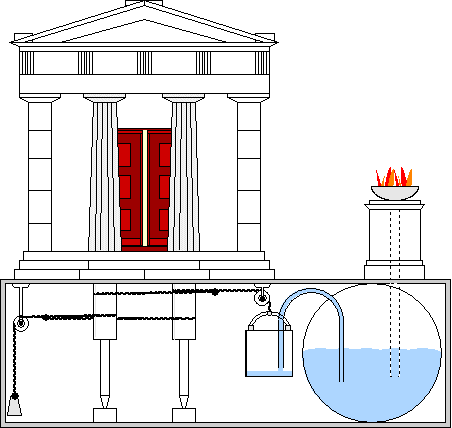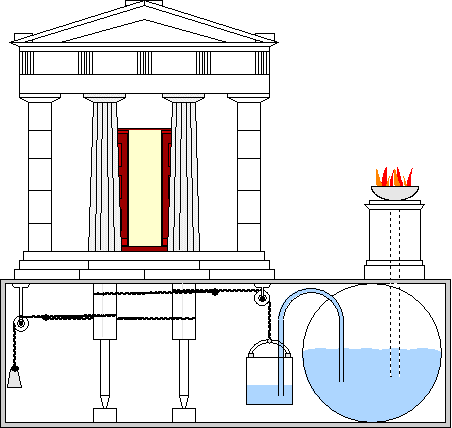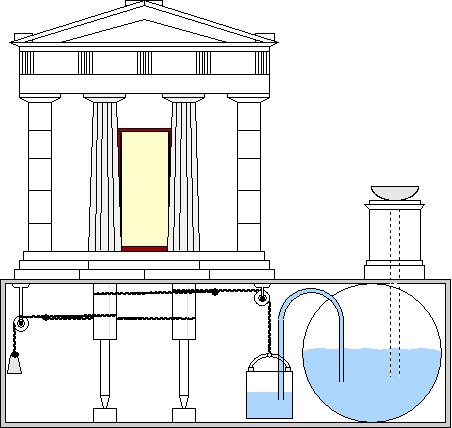
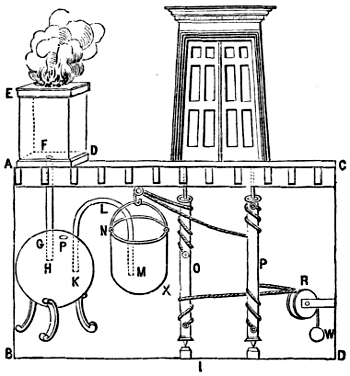
In Heron’s numerous surviving writings are designs for automata—machines operated by mechanical or pneumatic means. These included devices for temples to instill faith by deceiving believers with “magical acts of the gods,” for theatrical spectacles, and machines like a statue that poured wine. Among his inventions were:

♦ A windwheel operating a pipe organ—the first instance of wind powering a machine.

♦ The first automatic vending machine. When a coin was introduced through a slot on the top of the machine, a set amount of holy water was dispensed. When the coin was deposited, it fell upon a pan attached to a lever. The lever opened up a valve which let some water flow out. The pan continued to tilt with the weight of the coin until the coin fell off, at which point a counter-weight would snap the lever back up and turn off the valve.

♦ Mechanisms for the Greek theater, including an entirely mechanical puppet play almost ten minutes in length, powered by a binary-like system of ropes, knots, and simple machines operated by a rotating cylindrical cogwheel. The sound of thunder was produced by the mechanically-timed dropping of metal balls onto a hidden drum.

(Source: http://www.historyofinformation.com/expanded.php?id=16)

List of Heron’s works

•Pneumatica (Pneumatics), a treatise on the use of air, water, or steam

•Automatopoietica, about making automatic devices

•Belopoeica, on the constructions of machines of war

•Mechanics, describes mechanisms and simple machines

•Barulkos, discusses methods of lifting heavy weights.

•Dioptra, describes an instrument used in surveying and methods to measure length

•Catoptrica (Catoptrics), on light propagation and reflection, and on the use of mirrors.

•Cheirobalistra (On Catapults), about catapults

•Metrica, describes how to calculate surfaces and volumes of diverse objects

•Geometrica (Geometria), a collection of equations based on the first chapter of Metrica

•Stereometrica (i. and ii.), examples of 3-D calculations based on the second chapter of Metrica

•Geodaesia, a surveying analysis

•Mensurae, describes tools that can be used to conduct measurements based on Stereometrica and Metrica

•Definitiones (Definitions), containing definitions of terms for geometry

Research-Selection for NovoScriptorium: Philaretus Homerides